Weather radar has made many improvements in the last 10 years. There are more improvements on the way. All of the radars of the past and present work off the same basic principle: the radar equation below.

The basic concept of weather radar works off of the idea of a reflection of energy. The radar sends out a signal, as seen to the right, and the signal is then reflected back to the radar. The stronger that the reflected signal is, the larger the particle. For more basic information on weather radar, click here for a video from the Franklin Institute Science Muesum.

 

 

Image at right is courtesy COMET.

At the heart of the principle of radar is the radar equation .

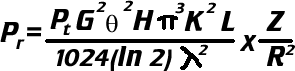
This equation involves variables that are either known or are directly measured. There is only one value that is missing, but it can be solved for mathematically. Below is the list of variables, what they are, and how they are measured.

Pr: Average power returned to the radar from a target. The radar sends up to 25 pulses and then measures the average power that is received in those returns. The radar uses multiple pulses since the power returned by a meteorological target varies from pulse to pulse. This is an unknown value of the radar, but it is one that is directly calculated.

Pt: Peak power transmitted by the radar. This is a known value of the radar. It is important to know because the average power returned is directly related to the transmitted power.

G: Antenna gain of the radar. This is a known value of the radar. This is a measure of the antenna's ability to focus outgoing energy into the beam. The power received from a given target is directly related to the square of the antenna gain.

: Angular beamwidth of the radar. This is a known value of the radar. Through the Probert-Jones equation it can be learned that the return power is directly related to the square of the angular beamwidth. The problem becomes that the assumption of the equation is that precipitation fills the beam for radars with beams wider than two degrees. It is also an invalid assumption for any weather radar at long distances. The lower resolution at great distances is called the aspect ratio problem.

H: Pulse Length of the radar. This is a known value of the radar. The power received from a meteorological target is directly related to the pulse length.

K: This is a physical constant. This is a known value of the radar. This constant relies on the dielectric constant of water. This is an assumption that has to be made, but also can cause some problems. The dielectric constant of water is near one, meaning it has a good reflectivity. The problem occurs when you have meteorological targets that do not share that reflectivity. Some examples of this are snow and dry hail since their constants are around 0.2.

L: This is the loss factor of the radar. This is a value that is calculated to compensate for attenuation by precipitation, atmospheric gases, and receiver detection limitations. The attenuation by precipitation is a function of precipitation intensity and wavelength. For atmospheric gases, it is a function of elevation angle, range, and wavelength. Since all of this accounts for a 2dB loss, all signals are strengthened by 2 dB.

: This is the wavelength of the transmitted energy. This is a known value of the radar. The amount of power returned from a precipitation target is inversely since the short wavelengths are subject to significant attenuation. The longer the wavelength, the less attenuation caused by precipitate.

Z: This is the reflectivity factor of the precipitate. This is the value that is solved for mathematically by the radar. The number of drops and the size of the drops affect this value. This value can cause problems because the radar cannot determine the size of the precipitate. The size is important since the reflectivity factor of a precipitation target is determined by raising each drop diameter in the sample volume to the sixth power and then summing all those values together. A ¼" drop reflects the same amount of energy as 64 1/8" drops even though there is 729 times more liquid in the 1/8" drops.

R: This is the target range of the precipitate. This value can be calculated by measuring the time it takes the signal to return. The range is important since the average power return from a target is inversely related to the square of its range from the radar. The radar has to normalize the power returned to compensate for the range attenuation.

Using a relationship between Z and R, an estimate of rainfall can be achieved. A base equation that can be used to do this is Z=200*R^1.6. This equation can be modified at the user's request to a better fitting equation for the day or the area.

For more information on the basic physics of Radar, check out the Cassini Radar Web Page.

Back to Main Radar Page

For questions or comments about this page, please visit our "Contact Us" page.

Created by Adam Frederick, webmaster@severewx.com
Content and Images (unless otherwise noted) Copyright 1999 Adam Frederick
Last updated 07/21/99 10:18 PM